环境影响评价工程师技术方法考试重点讲解（3）

河流水质数学模式预测方法：

1.河流稀释混合模式

（1）点源：河水、污水稀释混合方程。对于点源排放持久性污染物，河水与污水完全混合、反映河流稀释能力的方程为：

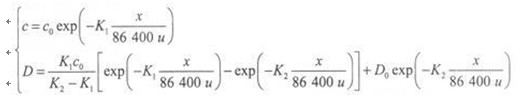
式中：C—污水与河水混合后的浓度，mg／L；

C_p—排放口处污染物的排放浓度，mg／L；   

Q_p—排放口处的废水排放量，mg／s。

C_h—河流上游某污染物的浓度，mg／L；

Q_h—河流上游的流量，mg／s；

例题 ：

计划在河边建一座工厂，该厂将以2.83m³／s的流量排放污水，污水中总溶解固体（总可滤残渣和总不可滤残渣）浓度为 1300mg／L，该河流平均流速υ为 0.457m／s，平均河宽W为13.73m，平均水深h为0.61m，总溶解固体浓度c_p为310mg／L，问该工厂的污水排入河后，总溶解固体的浓度是否超标（设标准为500mg／L）？

解析：C_p=310mg／L

河流的流量为 Q_P=υwh=0.457×13.72×0.61=3.82m³／s

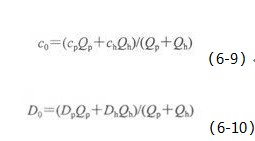
根据完全混合模型式，

混合后的浓度为

结论是河水中总溶解固体浓度超标。

（2）非点源方程：对于沿程有非点源（面源）分布入流的情形，可按下式计算河段污染物的浓度：

式中：

　　W_s——沿程河段内（x＝0到x＝x_s）非点源汇入的污染物总负荷量，kg/d；

　　Q——下游x距离处河段流量，m³/s；

　　Q_s——沿程河段内（x＝0到x＝x_s。）非点源汇入的水量，m³/s；

　　x_s——控制河段总长度，km；

x——沿程距离（0≤x≤x_s），km。

（3）考虑吸附态和溶解态污染指标耦合模型

当需要区分溶解态和吸附态的污染物在河流水体中的指标耦合，应加入分配系数的概念。

　　分配系数K_p的物理意义是在平衡状态下，某种物质在固液两相间的分配比例。

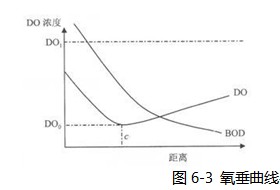
2.河流的一维稳态水质模式

对于溶解态污染物，当污染物在河流横向方向上达到完全混合后，描述污染物的输移、转化的微分方程为：

式中：

　　A——河流横断面面积：

　　Q——河流流量；

　　c——水质组分浓度；

　　D_L——综合的纵向离散系数；

　　S_L——直接的点源或非点源强度：

　　S_B——上游区域进入的源强；

　　S_K——动力学转化率，正为源，负为汇。

　　设定条件：稳态（ ＝0），忽略纵向离散作用，则上述微分方程的解为：                                       

C=C₀﹒exp[-Kx/(86400u)]                   （6-7）

式中：

　　c₀——初始浓度，mg/L；

　　u——河流流速，m/s；

　　x——沿河流方向距离，m；

c——位于污染源（排放口）下游x处的水质浓度，mg/L。